Introduction:

According to Wikipedia, tries can be defined as “an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings.” Now the definition sounds complex so I prefer to always use examples to illustrate what things would mean. For now, from a very high level its a tree structure whose nodes are used to store strings and the typical use of such datastructures are in string lookup / lexical sorting / doing incremental search etc.

In this post, I implemented tries and ternary trees to demonstrate the differences between the two datastructures and how they are created and traversed.

Since I am too lazy to draw the images myself, I have shamelessly stole the images from other sites. All credits to the original authors.

Ternary Trees:

The image above shows how a ternary tree would look. So every node in this tree essentially has lets say 26 or 52 (if we distinguish between lowercase and uppercase characters) children. Obviously things can be optimized to eliminate nodes which would never appear but for simplicity lets say we have that many child nodes.

Now lets say we have created this tree from a dictionary of words. The words which are there in the dictionary are as follows.

• are
• as
• dot
• news
• not
• zen

The above ternary tree shows how the datastructure would look when its created from the words above. So question is how would incremental search work with such a datastructure. So let’s say, someone presses ‘n’ on the keyboard.

So the root node is first looked up to see if it has any child with ‘n’. In this case it does find it. So then it does a Depth First Search from the node ‘n’ and it keeps on accumulating the child nodes (or the characters the child nodes represent). So in this case it could go to ‘e’ or ‘o’ respectively and so on and so forth.

So the 2 words it gets are “news” and “not”.

Now the user presses ‘e’. So, then ‘e’ is searched on all child nodes of ‘n’. Once the ‘e’ node is found again a DFS is done and the result is “ews”. So the user is only returned “news” and no other result.

Optimizing the search:

Obviously doing DFS at every node can quickly become slow and painful and hence we could cache the results of any previous dfs performed at that node and look at up. If it’s available then that can be returned directly.

Tries:

Although the exact classification of tries has been confusing around the web, for the purposes of this post lets assume that its a compressed ternary tree (Obviously do read up the actual definitions to be clear).

So lets look at a few cases from the image above. “d” –> “o” –> “t” have no child nodes in between. So we could safely collapse these to one node “dot”. The same goes for “ews” and “ot”. So the difference between this and the previous tree is that they it uses far fewer nodes and hence the dfs is faster, specially for longer words. It also reduces the memory requirements for storing this in memory.

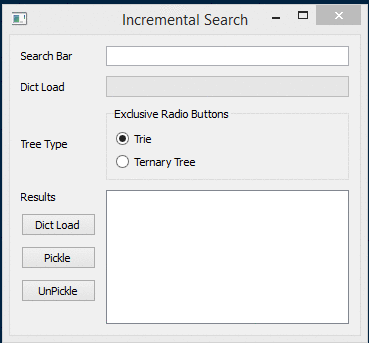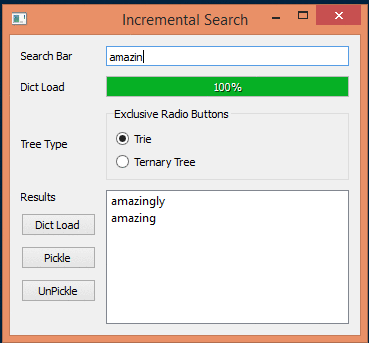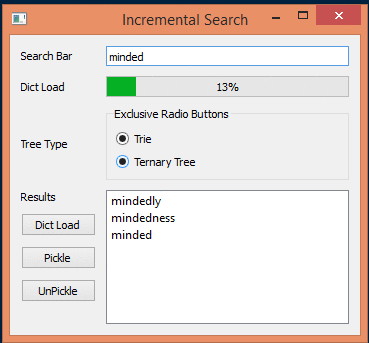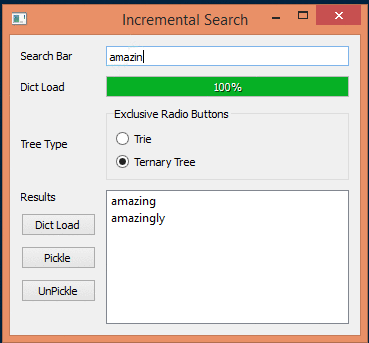
Implementation:

I have added UI which can compute the trees and store them as python pickle files. That way it doesn’t have to be recreated everytime and it can be loaded from disk. The code is far from perfect but does demonstrate the idea.